Ho preso alcuni dati forniti dalla Protezione civile riguardo il famigerato Coronavirus. Ho plottato il numero di morti e remitted (somma di morti più guariti) al variare del tempo.
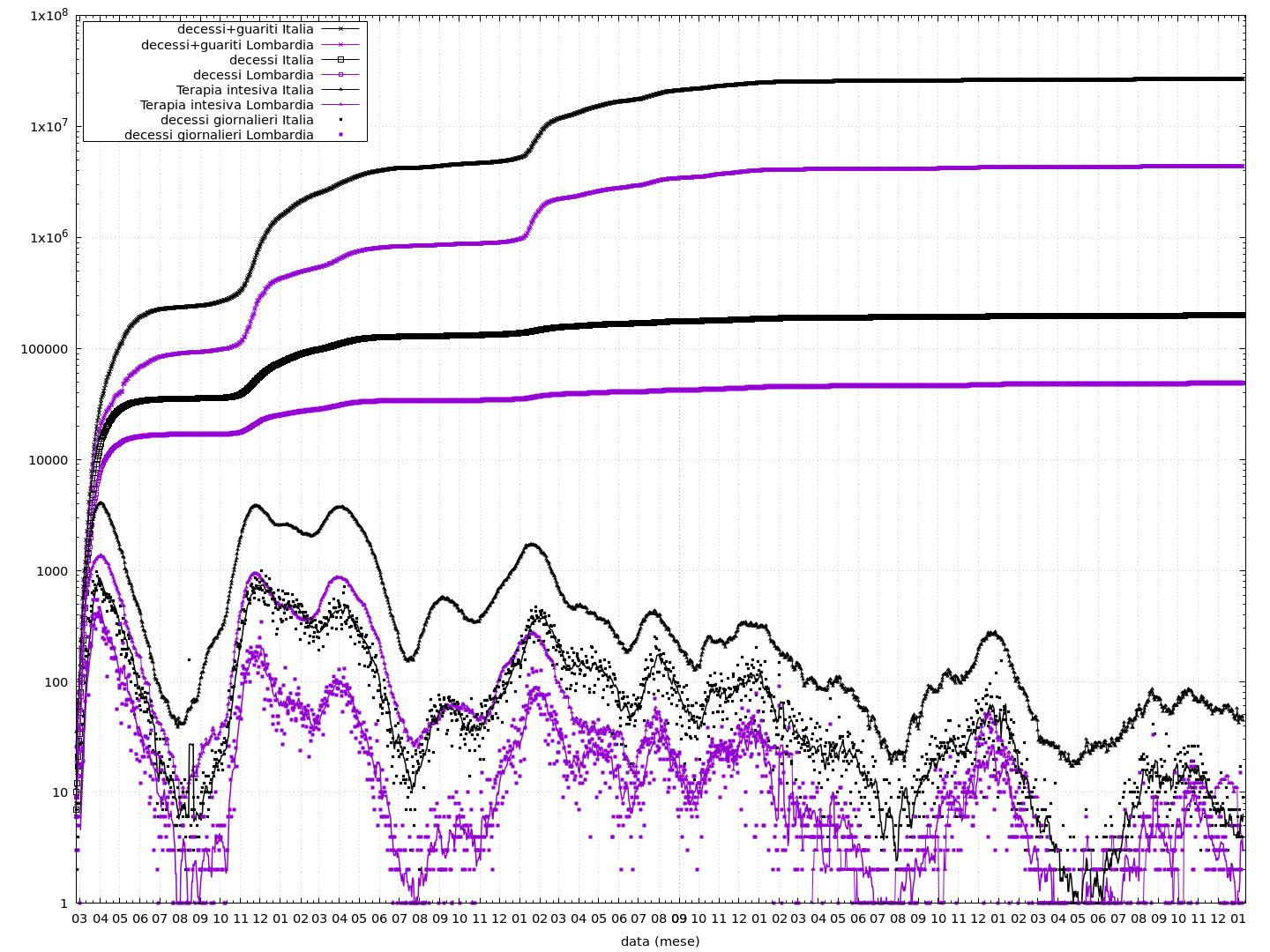
Visti in scala logaritmica per le y ci si accorge subito di una crescita esponenziale: le vittime raddoppiano ogni circa 3 giorni e decuplicano ogni 7-8 giorni.
Potete scaricare qui lo script per generare queste immagini.
Ho fatto questo grafico solo per esplorare un po' le funzionalità di gnuplot. Non ho la pretesa di affermare alcunché.
Aggiornamento Ho fatto in modo che questa immagine si aggiorni da sola.
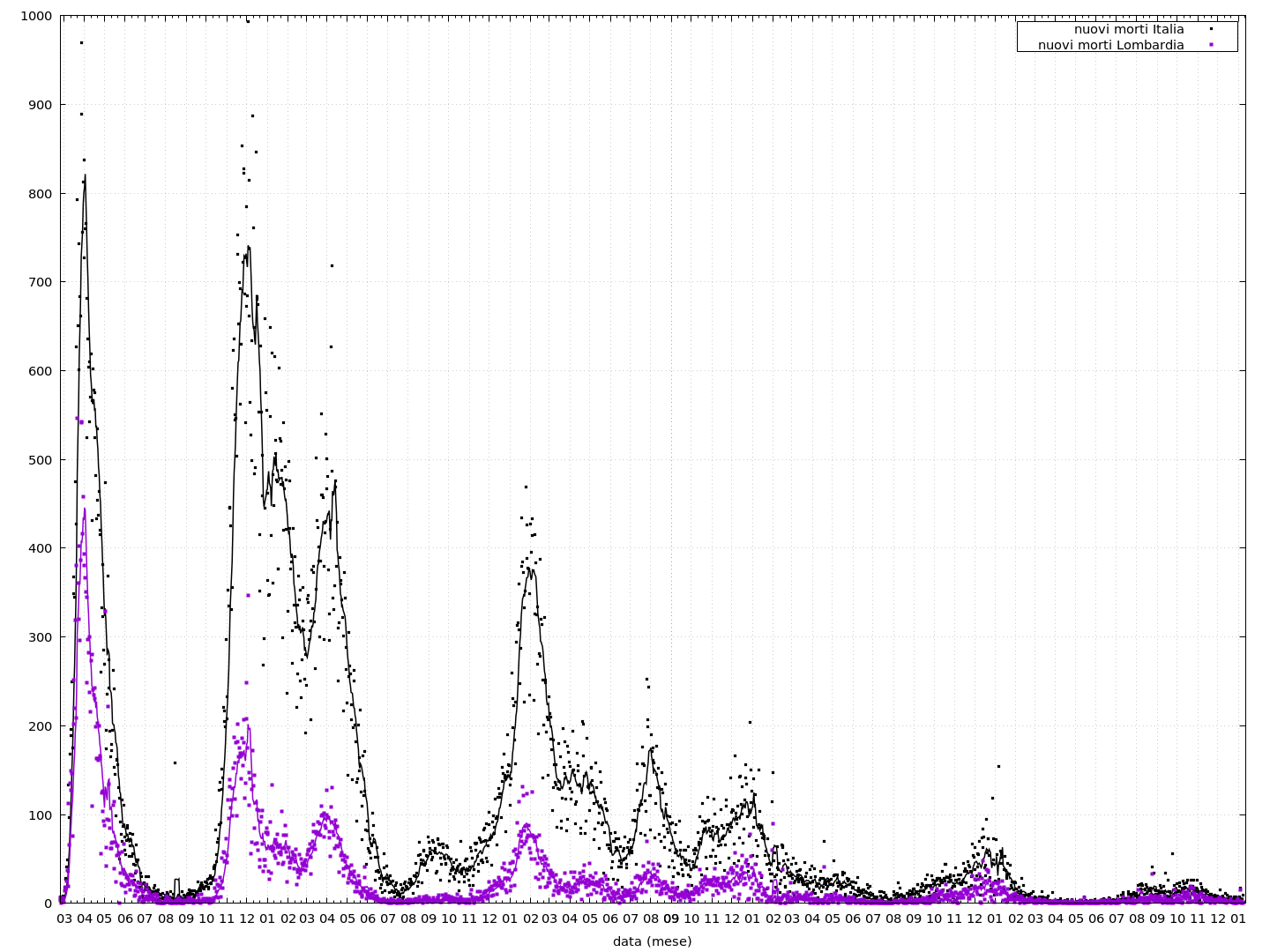
Aggiornamento 2 Nel grafico sopra ho aggiunto i morti giornalieri. Ho fatto anche il grafico (lineare) con solo i morti giornalieri.
Aggiornamento 3 Provo a fare una stima di tutte le vittime che mieterà questo virus usando il modello logistico. Prima di procedere dico subito che l'equazione logistica è un modello assai rudimentale e sono stati inventati vari modelli più sofisticati per lo studio della diffusione di epidemie. D'altro canto non ho grandi pretese nel fare queste previsioni, e per me la logistica va più che bene.
L'equazione differenziale logistica per la variabile y che rappresenta il numero di morti è
y'=ay(K-y)
dove a e K sono due costanti positive. Questa equazione ha due equilibri: quello banale y=0 (epidemia mai iniziata) e y=K (l'epidemia ha raggiunto il numero massimo dei morti. Se completiamo l'equazione con un dato iniziale compreso tra 0 e K i morti crescono e convergono asintoticamente a K. K è dunque il numero di morti alla fine dell'epidemia. Come stimare a e, soprattutto, K? Girando l'equazione otteniamo
(d log(y))/dt = y'/y = a(K-y),
dunque la derivata logaritmica rispetto al tempo di y dipende da y come una retta. Possiamo quindi fare il grafico di y'/y in funzione di y usando i dati forniti dalla protezione civile. La derivata y' è approssimata con i morti giornalieri.
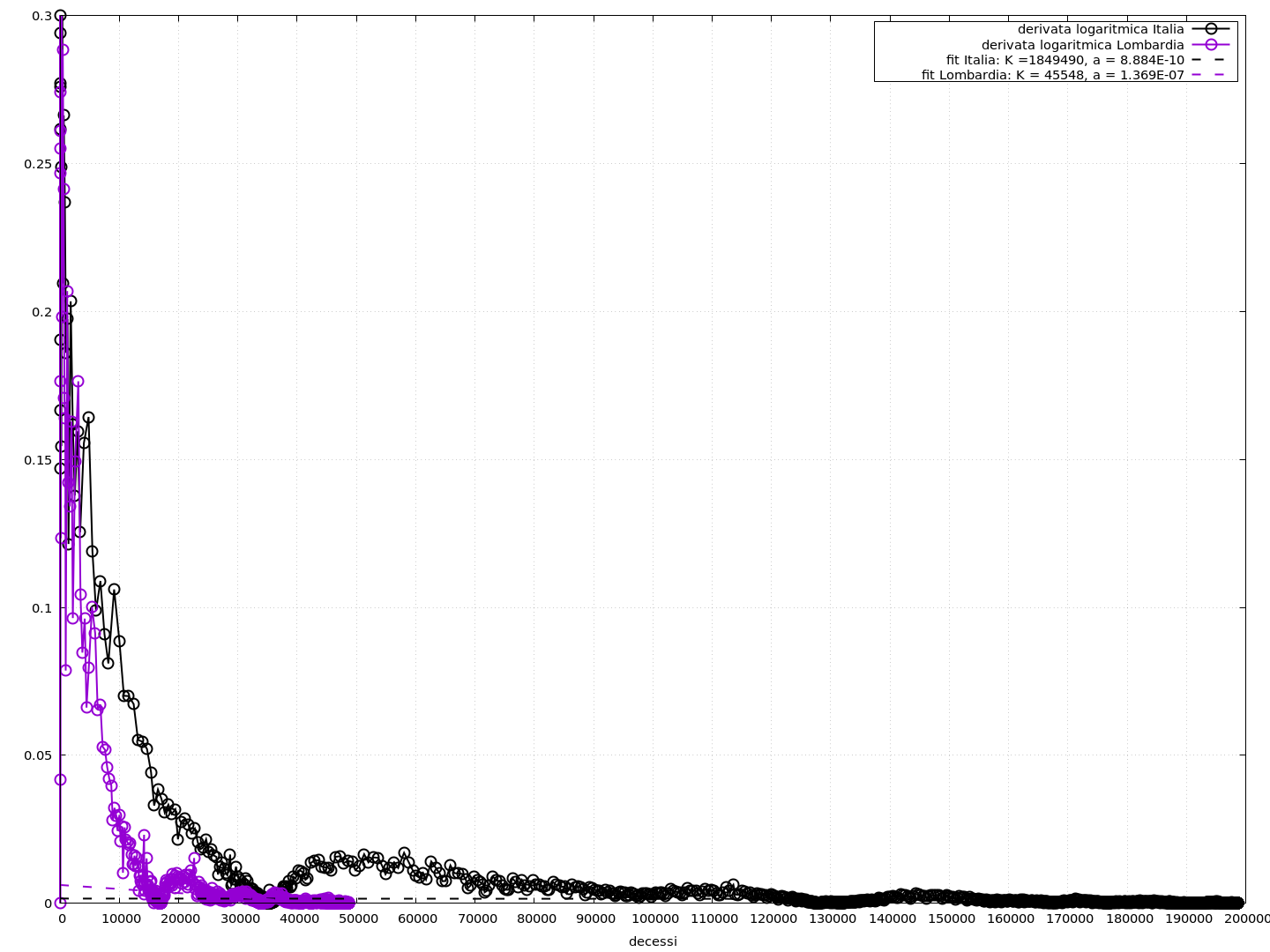
Facendo un fit lineare, calcolo i valori di a e K (ho considerato solo i dati in cui i morti sono più di 2000). Nella figura, in tratteggiato sono rappresentate le rette z=a(K-y) con i valori di a e K trovati per Italia e Lombardia.
P.S. Scrivere formule in Markdown non è poi così difficile.
Aggiornamento 4 Non faccio più il fit considerando solo i dati in cui i morti sono più di 2000, ma chiedo che siano più di 8000.